Применение технологии машинного обучения для прогнозирования оптической силы интраокулярных линз: генерализация диагностических данных

Полный текст

ОБОСНОВАНИЕ

Имплантация современных интраокулярных линз (ИОЛ) позволяет офтальмологам эффективно решать задачи хирургической реабилитации пациентов с катарактой. Однако степень улучшения зрительных функций пациента напрямую связана с точностью предоперационного расчёта оптической силы ИОЛ. В связи с этим в офтальмологии используются различные формулы для расчёта этого показателя. К наиболее известным относятся формулы SRK II, SRK/T, Hoffer-Q, Holladay II, Haigis, Barrett [1–7]. Все они хорошо работают для «среднего пациента», но не являются в достаточной степени адекватными на границах диапазонов входных переменных. Есть у них и другие недостатки: во-первых, они не учитывают нестационарность объектов и не позволяют менять настройки при вводе новых эмпирических данных, как, например, при локализации модели; во-вторых, количество учитываемых входных факторов оказывается явно недостаточным. Эти обстоятельства приводят к множеству локальных поправок к приведённым формулам и их постоянной адаптации [2, 8].

Одна из первых формул для расчёта оптической силы ИОЛ, основанная на законах оптики и данных схематического глаза, принадлежит выдающемуся российскому офтальмологу С.Н. Фёдорову (1967) [1, 2]. В последующие годы, вплоть до настоящего времени, наиболее часто для расчёта оптической силы ИОЛ в офтальмологической практике использовались формулы SRK/T, SRK II, Hoffer-Q, Holladay II, Haigis и Barrett [3–7]. Самые ранние формулы для расчёта оптической силы ИОЛ за рубежом появились в конце 1970-х — начале 1980-х гг. Они были либо теоретическими, либо регрессионными. В предпочтениях хирургов преобладали регрессионные формулы, одна из самых успешных — SRK, разработанная D.R. Sanders, J.A. Retzlaff и M.C. Kraff [3–5].

В настоящее время наблюдается беспрецедентное развитие систем искусственного интеллекта на основе искусственных нейронных сетей (ИНС), которые путём глубокого обучения с использованием значительных по объёмам массивов эмпирических данных позволяют строить адекватные модели практически в любой предметной области, в том числе в биологии и медицине [9–12]. Кроме того, современные офтальмологические центры за последние десятилетия создали хранилища данных о пациентах, включающие десятки и сотни тысяч записей оцифрованных показателей.

В этой ситуации можно предполагать, что радикальным методом решения проблемы предоперационного расчёта ИОЛ стало бы построение интеллектуальной экспертной системы, ядром которой была бы математическая модель, построенная с помощью ИНС (ИНС-модель). Такая модель могла бы обучаться на основе поступающих из хранилища данных, что позволило бы учесть значительно большее число значимых входных факторов и региональную специфику пациентов, по сравнению с известными формулами. Поэтапное переучивание ИНС-модели на вновь поступающих из хранилища данных, а при необходимости и модификация её структуры обеспечили бы её адаптивность и сняли проблему учёта нестационарности объекта и локализации модели.

Первым этапом построения такой интеллектуальной экспертной системы является решение принципиального вопроса о генерализации (возможности обобщения) эмпирических данных значительного числа пациентов с помощью ИНС-модели, выявление значимых наблюдаемых входных факторов и сравнение адекватности такой модели с известными формулами [1–7].

ЦЕЛИ

Изучить возможности генерализации значительного количества эмпирических данных по расчёту ИОЛ, полученных в одном из офтальмологических центров России в результате лечения пациентов, с использованием глубокого обучения ИНС-моделей; выявить наиболее значимые наблюдаемые входные факторы, оказывающие существенное влияние на погрешность предоперационного расчёта ИОЛ; сравнить погрешности расчётов по ИНС-моделям с известными формулами.

Погрешности расчёта оптической силы интраокулярных линз

Ранее мы сравнивали погрешности в использовании некоторых формул на основе значительного количества эмпирических данных, предоставленных в обезличенном виде Тамбовским филиалом Федерального государственного автономного учреждения «Национальный медицинский исследовательский центр “Межотраслевой научно-технический комплекс «Микрохирургия глаза» имени академика С.Н. Фёдорова”» Министерства здравоохранения Российской Федерации [13]. Исходные данные были получены в конце 2014 года. Первоначальное количество записей составило 28 940. Каждая запись содержала следующие параметры:

• анонимный номер пациента;
• дата операции;
• торговая марка и оптическая сила имплантированной ИОЛ;
• возраст пациента;
• длина глаза;
• требуемая оптическая сила ИОЛ для коррекции аномалий рефракции и астигматизма (сфера и цилиндр);
• дополнительная информация, связанная с положением ИОЛ в глазу.

Количество обработанных записей составило 11 701. При этом 17 239 записей не были обработаны в связи с отсутствием параметров линзы или некорректностью данных в полях.

Формулы Haigis, Holladay, SRK II и SRK/T рассматривались как наиболее близкие к эмпирическим данным.

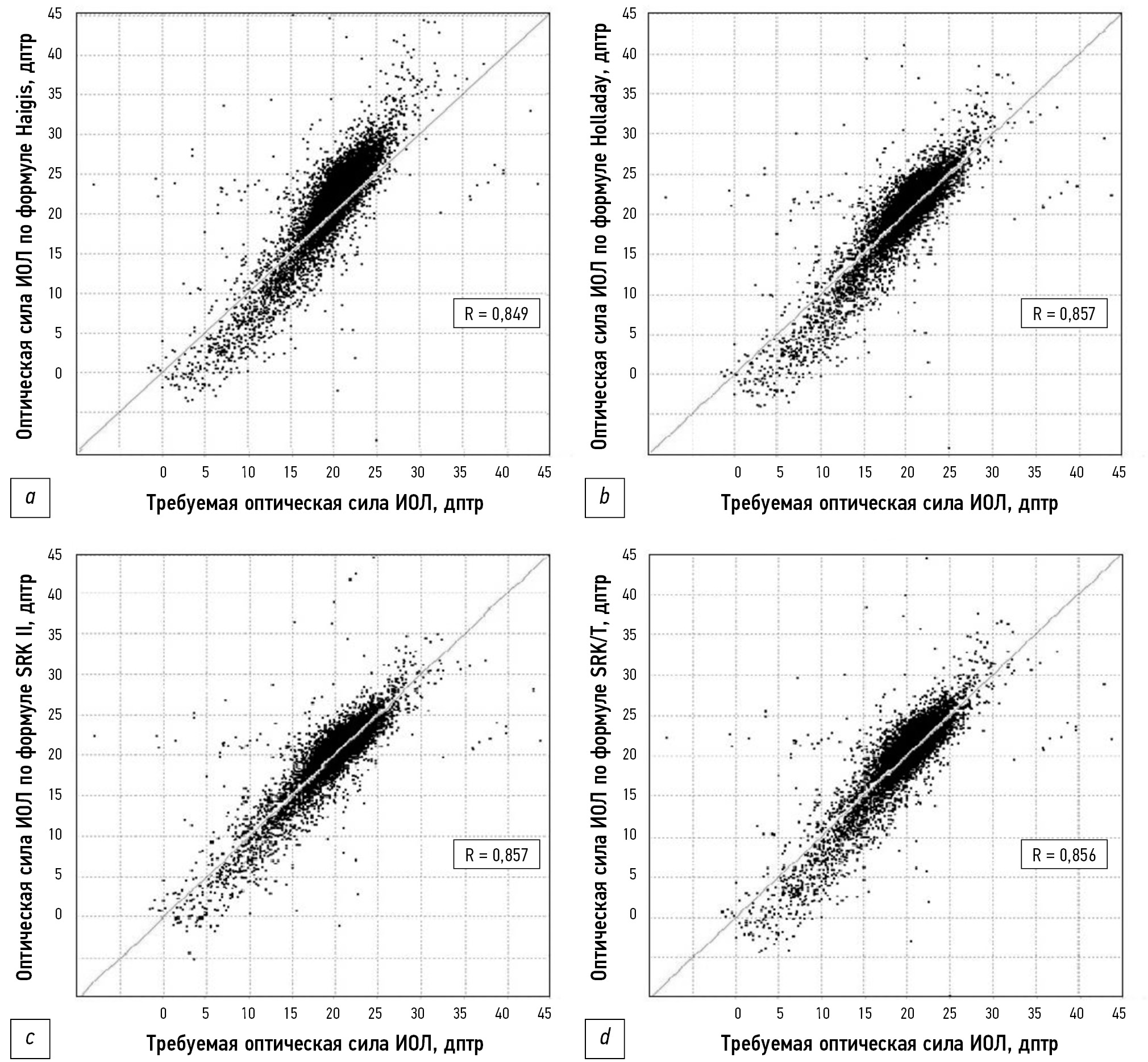
Значения средних относительных погрешностей при расчёте ИОЛ представлены в табл. 1. На рис. 1 показана корреляционная зависимость требуемой и рассчитанной оптической силы ИОЛ по данным формулам. При вычислении средней оптической силы ИОЛ все формулы дают результаты, близкие к требуемым, однако при крайних значениях наблюдается значительный разброс относительно требуемых величин.

 

Таблица 1. Сравнение погрешностей расчёта оптической силы интраокулярных линз, полученных при использовании различных формул

Формула	Средняя относительная погрешность расчёта интраокулярных линз, %
Формула Haigis	15,6
Формула Holladay	13,4
Формула SRK II	11,7
Формула SRK/T	12,5

 

Рис. 1. Корреляционная зависимость требуемой оптической силы интраокулярных линз (по горизонтальной оси) и их рассчитанной оптической силы (по вертикальной оси согласно формулам) для 11 701 пациента: а — Haigis; b — Holladay; c — SRK II; d — SRK/T. ИОЛ — интраокулярные линзы. Коэффициенты корреляции представлены на графиках.

 

Так, существенное расхождение значений наблюдается в угле наклона зависимости относительно диагонали, соответствующей точным расчётам (рис. 1, a, b, d). Во всех исследованных формулах в качестве входных величин используются три параметра: длина глаза в мм (L), среднее арифметическое меридианов в мм (K) и глубина передней камеры как параметр линзы. Это обстоятельство неизбежно предполагает наличие других факторов (возможно, ненаблюдаемых). Их воздействие на оптическую силу ИОЛ обусловило перечисленные особенности расчётов.

В том же исследовании [13] мы представили оптимизированную регрессионную формулу, полученную путём минимизации средней квадратичной погрешности с помощью методов нелинейного программирования для 11 701 пациента. Нам удалось снизить среднюю относительную погрешность до 10,6% за счёт введения четвёртой переменной. Это означает, что нужно учитывать дополнительные входные переменные и, в идеале, всю необходимую информацию о пациенте. В этом случае оптимальным инструментом для прогнозирования оптической силы ИОЛ будет использование ИНС-моделей.

Наиболее близким к нашей работе является исследование T. Yamauchi и соавт. [14], направленное на описание использования машинного обучения для прогнозирования послеоперационной рефракции при удалении катаракты и сравнения точности модели с традиционными формулами при расчёте оптической силы ИОЛ. Обучающая выборка включала данные 2010 пациентов (3331 глаза). Коэффициенты модели оптимизировались с помощью обучения по данным. Затем возникновение послеоперационной рефракции авторы прогнозировали с использованием общепринятых формул: SRK/T, Haigis, Holladay II, Hoffer-Q и Barrett Universal II formula (BU-II). Абсолютные погрешности некоторых методов машинного обучения были ниже, чем при вычислении по формулам. Однако статистически значимой разницы не наблюдалось.

Полученные результаты являются, на наш взгляд, ожидаемыми, так как авторы не использовали дополнительных входных параметров, а машинное обучение и метод наименьших квадратов, обычно используемый при параметрической идентификации формул, как правило, приводят к сопоставимым результатам. В настоящем исследовании мы анализируем возможности использования ИНС-моделей для прогнозирования оптической силы ИОЛ с использованием гораздо большего числа входных параметров.

Работа над расчётами ИОЛ продолжается в связи с:

• необходимостью уменьшения погрешностей;
• появлением данных о новых факторах, которые не учитывались в предыдущих расчётах (ранее учитывались только 4 входных фактора по сравнению с нынешними 26);
• желанием разработать адаптивную модель расчёта ИОЛ, которая могла бы учитывать возможную нестационарность при поступлении новых данных;
• стремлением создать экспертную систему с динамическим поступлением данных и её поэтапным обучением с использованием ИНС-моделей.

МАТЕРИАЛЫ И МЕТОДЫ

В 2021 году офтальмолог К.К. Сырых представил первичные данные в виде обезличенных результатов предоперационных и послеоперационных обследований пациентов. Исходный файл данных, использованный для построения ИНС-модели, включал 455 записей: 26 столбцов входных факторов и один столбец — выходной фактор — расчёт ИОЛ (дптр). Для удобства работы входные параметры обозначены через x₁–x₂₆, выходной параметр — через Y. Входные переменные представлены в табл. 2.

 

Таблица 2. Входные параметры для построения модели, основанной на искусственной нейронной сети

Параметр	Значение	Параметр	Значение
x1	пол	x14	длина глаза (оптическая биометрия, мм)
x2	острота зрения без коррекции до операции	x15	острота зрения без коррекции после операции
x3	сферический компонент рефракции по данным визометрии до операции	x16	сферический компонент рефракции по данным визометрии после операции
x4	цилиндрический компонент рефракции по данным визометрии до операции	x17	цилиндрический компонент рефракции по данным визометрии после операции
x5	ось цилиндра по данным визометрии до операции	x18	ось цилиндра по данным визометрии после операции
x6	острота зрения с коррекцией до операции	x19	острота зрения с коррекцией после операции
x7	ось сильного меридиана роговицы до операции	x20	ось сильного меридиана роговицы после операции
x8	рефракция сильного меридиана роговицы до операции	x21	рефракция сильного меридиана роговицы после операции
x9	ось слабого меридиана роговицы до операции	x22	ось слабого меридиана роговицы после операции
x10	рефракция слабого меридиана роговицы до операции	x23	рефракция слабого меридиана роговицы после операции
x11	сферический компонент рефракции по данным рефрактометрии до операции	x24	сферический компонент рефракции по данным рефрактометрии после операции
x12	цилиндрический компонент рефракции по данным рефрактометрии до операции	x25	цилиндрический компонент рефракции по данным рефрактометрии после операции
x13	ось цилиндра по данным рефрактометрии до операции	x26	ось цилиндра по данным рефрактометрии после операции

 

Для удобства построения ИНС-моделей использовалась программа-симулятор, ранее разработанная авторами [15].

РЕЗУЛЬТАТЫ

Одним из наиболее сложных вопросов при разработке ИНС-моделей является принятие гипотезы о структуре (архитектуре) сети.

Известно, что при использовании теорем А.Н. Колмогорова [16, 17] часто получается структура ИНС-модели, являющейся избыточной. Как правило, такая модель хорошо представляет выходную переменную в узловых точках, но обладает слабой прогностической способностью.

В работе [18] мы предложили конструктивный алгоритм, позволяющий увеличивать количество нейронов в скрытом слое и число скрытых слоёв до достижения определённых условий. При этом используются линейные, квадратичные, кубические и другие передаточные функции нейронов, а не общепринятые сигмоидальные. Наш подход основан на разложении функции нескольких переменных в ряд Тейлора (1)–(2). При разложении функции большого числа переменных необходимо сначала ввести дифференциальный оператор:

 ${\mathit{T}}^{\mathit{k}}\mathbf{=}\mathbf{\sum }_{\mathbf{m}\mathbf{=}\mathbf{1}}^{\mathbf{n}}{\mathbf{(}{\mathbf{x}}^{\left(m\right)}\mathbf{-}{\mathbf{x}}_{\mathbf{0}}^{\left(m\right)}\mathbf{)}}^{\mathbf{k}}\frac{{\mathbf{\partial }}^{\mathbf{k}}}{\mathbf{\partial }{\mathbf{x}}_{\mathbf{k}}^{\left(m\right)}}$(1)

Разложение функции $f(x^{\left(1\right)},x^{\left(2\right)}, ... ,x^{\left(n\right)})$ в ряд Тейлора имеет следующий вид:

$f\mathit{(}{x}^{\left(1\right)}\mathit{,}\mathit{ }{x}^{\left(2\right)}\mathit{,}\mathit{ }\mathit{.}\mathit{.}\mathit{.}\mathit{ }\mathit{,}\mathit{ }{x}^{\left(n\right)}\mathit{)}\mathit{ }=$ 

$=f\mathit{(}{x}_{\mathit{0}}^{\left(1\right)}\mathit{,}\mathit{ }{x}_{\mathit{0}}^{\left(2\right)}\mathit{,}\mathit{ }\mathit{.}\mathit{.}\mathit{.}\mathit{ }\mathit{,}\mathit{ }{x}_{\mathit{0}}^{\left(n\right)}\mathit{)}\mathit{ }+$                  (2)

$+\sum _k^p=1\frac{T^k(x^{\left(1\right)}, x^{\left(2\right)}, ... , x^{\left(n\right)})}{k!}+$

$+R_p(x^{\left(1\right)}, x^{\left(2\right)}, ... , x^{\left(n\right)})$

Такой подход позволяет получать нейронные сети с относительно простой архитектурой, обладающие хорошими аппроксимирующими (генерализующими) и прогностическими способностями.

ИНС-модель, построенная в соответствии с формулами (1) и (2), имеет 4 слоя:

1) слой входных нейронов;

2) функциональный скрытый слой, соответствующий нескольким членам ряда Тейлора;

3) суммирующий скрытый слой;

4) выходной слой.

Функциональный скрытый слой содержит нейроны с передаточными функциями, соответствующими членам ряда Тейлора: линейными (первый порядок), квадратичными (второй порядок) и кубическими (третий порядок). Суммирующий скрытый слой содержит один линейный нейрон, его основная функция — вычисление суммы нескольких членов ряда и прибавление к ним постоянного значения. Такая архитектура позволила добиться приемлемой точности ИНС-модели.

В качестве функции потерь использовали сумму квадратов отклонений модельных и эмпирических значений.

При обучении моделей на основе эмпирических данных были выбраны следующие методы оптимизации: метод стохастического градиента, простой градиентный метод и безградиентные методы покоординатного спуска Гаусса–Зейделя и Монте-Карло, которые использовались в интерактивном режиме.

Обучение ИНС-модели на основе данных по ИОЛ начали с сети, представляющей собой 26 входных нейронов и один линейный нейрон в скрытом слое. Такая конструкция соответствовала свободному и первому членам в формулах (1) и (2). Учитывая рекомендации предыдущих исследований [8–11], процесс обучения модели проводили на 70% всей выборки, прогностическую способность ИНС-модели оценивали на оставшихся 30% выборки. Данные для обучения и проверки адекватности модели выбирали из общей таблицы в произвольном порядке с равномерным распределением случайных величин.

Результаты обучения этой простой модели показаны на рис. 2. Истинную оптическую силу данного типа ИОЛ для получения эмметропии в каждом случае определяли как сумму оптической силы имплантированной ИОЛ и результирующей рефракционной погрешности. Погрешность рефракции рассчитывали с помощью ретроспективного анализа в период от 1 до 6 месяцев после операции.

 

Рис. 2. Корреляция расчётных (Y_mod) и эмпирических данных (Y_tab) для модели первого порядка. Коэффициент парной корреляции — 0,84; средняя относительная погрешность — 11,9%.

 

По уровню средней относительной погрешности полученные результаты сопоставимы с классическими формулами, однако в данном случае для прогнозирования оптической силы ИОЛ мы использовали линейную функцию 26 переменных. При этом коэффициент парной корреляции расчётных и эмпирических данных составил 0,71, а средняя относительная погрешность — 11,9%.

Коэффициенты синаптических связей для каналов линейной модели представляют собой чувствительность каналов, значения которых могут быть использованы для оценки степени их влияния на выходную переменную. Численные эксперименты показали, что не менее 12–15 входных факторов (доступных офтальмологу) существенно влияют на предоперационные расчёты оптической силы ИОЛ. Следовательно, наши предположения относительно необходимости учёта большего числа входных величин для снижения погрешности расчёта полностью подтвердились. Ясно также, что значительные погрешности классических формул [3–7] тоже могут быть связаны с наличием большего числа входных факторов, которые в этих формулах являются ненаблюдаемыми.

Значения некоторых факторов (например, x₁₆, x₂₁, x₂₃ и x₂₄) становятся известны только после операции. Однако они хорошо коррелируют с аналогичными факторами до операции, их значения поэтому хорошо предсказуемы.

Следуя нашему алгоритму [18], мы изменили структуру ИНС-модели таким образом, чтобы наряду с линейным нейроном в скрытом слое присутствовал и квадратичный нейрон. Обучение такой ИНС-модели аналогичными численными методами нелинейного программирования позволило снизить среднюю относительную погрешность до 5%. Таким образом, предыдущие результаты удалось улучшить в 2 раза. При этом коэффициент парной корреляции составил 0,97, а средняя относительная погрешность — 4,8% (рис. 3).

 

Рис. 3. Корреляция расчётных (Y_mod) и эмпирических данных (Y_tab) модели второго порядка. Коэффициент парной корреляции — 0,97; средняя относительная погрешность — 4,8%.

 

Следуя указанной логике, мы также построили ИНС-модель третьего порядка, содержащую в скрытом слое нейроны с линейной, квадратичной и кубической передаточными функциями. Обучение такой ИНС-модели аналогичными численными методами нелинейного программирования позволило снизить среднюю относительную погрешность до уровня 3,5%, при коэффициенте парной корреляции 0,98 (рис. 4).

 

Рис. 4. Корреляция расчётных (Y_mod) и эмпирических данных (Y_tab) для модели третьего порядка. Коэффициент парной корреляции — 0,98; средняя относительная погрешность — 3,5%.

 

Необходимо отметить, что число степеней свободы данной ИНС-модели, равное количеству синаптических связей (26×3+3=81), существенно меньше, чем количество записей в обучающей выборке. Это обстоятельство указывает на хорошую генерализуемость эмпирических данных по расчёту оптической силы ИОЛ с использованием ИНС-моделей.

В табл. 3 приведены результаты сравнения различных методов расчёта оптической силы ИОЛ. Таким образом, при использовании ИНС-моделей и значительно большего числа входных переменных средняя относительная погрешность расчётов может быть снижена более чем в два раза по сравнению с традиционными методами.

 

Таблица 3. Результаты сравнения средних относительных погрешностей расчётов оптической силы интраокулярных линз и коэффициентов корреляции расчётных и эмпирических данных для различных методов

Формула или ИНС-модель	Средняя относительная погрешность, %	Коэффициент корреляции расчётных и эмпирических данных
Формула Haigis	15,6	0,85
Формула Holladay	13,4	0,86
Формула SRK II	11,7	0,86
Формула SRK/T	12,5	0,86
Линейная ИНС-модель	11,9	0,84
Нелинейная ИНС-модель второго порядка	4,8	0,98
Нелинейная ИНС-модель третьего порядка	3,5	0,99

 

ОБСУЖДЕНИЕ

Следующим этапом исследований в этом направлении должен быть сбор значительно большего числа обезличенных данных пред- и послеоперационного обследования пациентов, так как методы глубокого машинного обучения нуждаются в существенных по объёму обучающих выборках, после чего модели должны проходить процедуру валидации на тестовых выборках [11–14]. Если в системе имеются ещё и гиперпараметры (параметры, которые должны быть заданы «сверху», и от удачного введения которых существенно зависит решение задачи), то должна использоваться и третья, дополнительная проверочная выборка данных. Наличие таких данных позволит построить интеллектуальную экспертную систему предоперационного расчёта ИОЛ. Некоторые принципы построения такой системы мы уже описывали [19].

ЗАКЛЮЧЕНИЕ

Показана принципиальная возможность генерализации значительного количества эмпирических данных по расчёту оптической силы ИОЛ с использованием глубокого обучения ИНС-моделей, имеющих значительно большее количество входных переменных, чем при использовании традиционных формул и методов. Выявление наиболее значимых наблюдаемых факторов, оказывающих существенное влияние на целевой показатель, и их включение в ИНС-модель позволяют снизить погрешность расчётов более чем в 2 раза. Способность моделей на основе ИНС к хорошей генерализации данных открывает возможности создания интеллектуальной экспертной системы с динамическим поступлением новых данных и поэтапным глубоким машинным обучением интеллектуального ядра. Основной особенностью такой системы по сравнению с использованием традиционных формул расчёта является её адаптивность, позволяющая решать проблемы нестационарности объекта и локализации вследствие наличия в ней обратной связи. В настоящее время разработанная ИНС-модель используется в режиме ассистента офтальмолога в сочетании с другими инструментами для предоперационного расчёта оптической силы ИОЛ.

ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ

Источник финансирования. Авторы заявляют об отсутствии внешнего финансирования при проведении исследования.

Конфликт интересов. Авторы декларируют отсутствие явных и потенциальных конфликтов интересов, связанных с публикацией настоящей статьи.

Вклад авторов. Все авторы подтверждают соответствие своего авторства международным критериям ICMJE (все авторы внесли существенный вклад в разработку концепции, проведение исследования и подготовку статьи, прочли и одобрили финальную версию перед публикацией).

Наибольший вклад распределён следующим образом: А.А. Арзамасцев — концепция исследования, обработка данных, расчёты на основе ИНС-моделей, написание рукописи, редактирование рукописи; О.Л. Фабрикантов — концепция исследования, анализ литературы, редактирование рукописи; Н.А. Зенкова — обработка данных, анализ литературы, редактирование рукописи; С.В. Беликов — подготовка датасета, поиск публикаций.

ADDITIONAL INFO

Funding source. This study was not supported by any external sources of funding.

Competing interests. The authors declare that they have no competing interests.

Authors’ contribution. All authors made a substantial contribution to the conception of the work, acquisition, analysis, interpretation of data for the work, drafting and revising the work, final approval of the version to be published and agree to be accountable for all aspects of the work.

A.A. Arzamastsev — research concept, data processing, writing the manuscript, editing the manuscript; O.L. Fabrikantov — research concept, literature analysis, editing the manuscript; N.A. Zenkova — data processing, literature analysis, editing the manuscript; S.V. Belikov — preparing the dataset, searching for publications.

Об авторах

Александр Анатольевич Арзамасцев

Воронежский государственный университет; Национальный медицинский исследовательский центр «Межотраслевой научно-технический комплекс “Микрохирургия глаза” имени академика С.Н. Федорова»

Email: arz_sci@mail.ru
ORCID iD: 0000-0001-6795-2370
SPIN-код: 4410-6340

д-р техн. наук, профессор

Россия, Воронеж; Тамбов

Олег Львович Фабрикантов

Национальный медицинский исследовательский центр «Межотраслевой научно-технический комплекс “Микрохирургия глаза” имени академика С.Н. Федорова»

Email: fabr-mntk@yandex.ru
ORCID iD: 0000-0003-0097-991X
SPIN-код: 9675-9696

д-р мед. наук, профессор

Россия, Тамбов

Наталья Александровна Зенкова

Тамбовский государственный университет имени Г.Р. Державина

Email: natulin@mail.ru
ORCID iD: 0000-0002-2325-1924
SPIN-код: 2266-4168

канд. психол. наук, доцент

Россия, Тамбов

Сергей Вячеславович Беликов

Национальный медицинский исследовательский центр «Межотраслевой научно-технический комплекс “Микрохирургия глаза” имени академика С.Н. Федорова»

Автор, ответственный за переписку.
Email: pvt.leopold@gmail.com
ORCID iD: 0000-0002-4254-3906
SPIN-код: 5553-8398

MD

Россия, Тамбов

Список литературы

Дополнительные файлы