Проверка гипотез исследования с использованием языка R

Полный текст

ВВЕДЕНИЕ

Для современных учёных становятся всё более важными компетенции в области статистической обработки данных. В 1983 году для понимания 2/3 из 760 научных публикаций престижного New England Journal of Medicine читателю было достаточно владеть базовыми понятиями описательной статистики (процент, среднее значение и стандартное отклонение) и одним методом статистической проверки гипотез (t-критерий Стьюдента) [1]. Со временем научное сообщество столкнулось с ограниченностью такого подхода к анализу данных. В 2014 году Journal of American Medical Association анонсировал специальную серию выпусков, направленную на разбор методов статистического анализа для врачей-клиницистов¹. Сегодня в открытом доступе можно найти обзорные работы не только по базовым аспектам анализа данных [2], но и выбору подходящего метода их обработки [3]. Более того, в 2019 году опубликован подробный чек-лист по использованию статистических методов в биомедицинских исследованиях (Statistical Analysis Methods in Biomedical Research) [4]. Однако практическое применение методов анализа данных оставалось бы по-прежнему нетривиальной задачей, если бы не активная разработка программ для его автоматизации.

На фоне большого числа платных программ статистического анализа и наличия коммерческих предложений обработки данных «под ключ» очевидными преимуществами открытого программного обеспечения (open-source software) являются доступность и многофункциональность [5]. Наиболее широкими возможностями среди бесплатных решений обладает язык программирования и соответствующее программное обеспечение R [6], доступное в виде минималистичного консольного интерфейса [7] или полноценной среды разработки RStudio/Posit [8].

Цель настоящего материала ― познакомить читателя с базовыми операциями в R на примере задачи из реальной практики: сравнения эффективной дозы, полученной пациентами при проведении стандартной компьютерной томографии (КТ) и низкодозной компьютерной томографии (НДКТ) при COVID-19. Актуальность задачи основана на необходимости мониторинга лучевой нагрузки [9], в том числе в связи с нарастанием количества выполняемых лучевых исследований [10] и вследствие этого важности разработки [11] и клинической апробации [12, 13] протоколов НДКТ.

При проведении статистического анализа необходимо придерживаться основополагающих этапов.

Постановка задачи и формулировка нулевой гипотезы анализа

Нулевая гипотеза ― отправная точка статистического анализа. Для задач сравнения двух групп нулевая гипотеза (Н₀) формулируется следующим образом: «Статистически значимые различия отсутствуют». В настоящем примере проводилось сравнение эффективной дозы облучения пациентов для двух типов КТ-исследования (полнодозной и низкодозной) при COVID-19. Другими словами, формулировка Н₀ для данной задачи: «Лучевая нагрузка при КТ и НДКТ сопоставима».

Необходимо также помнить про «альтернативную гипотезу» (Н₁) ― это гипотеза-антагонист Н₀, они должны быть взаимоисключающими. В данном примере альтернативная гипотеза будет звучать так: «Эффективная доза облучения пациентов с COVID-19 при КТ и НДКТ статистически значимо отличается».

Результатом проверки нулевой гипотезы в статистике является так называемое p-value, т.е. вероятность ошибочно отвергнуть Н₀. Это значение можно интерпретировать следующим образом: «Если мы многократно повторим эксперимент и отвергнем нулевую гипотезу, то ошибемся в p-value из 100% случаев». Например, для p-value 0,03 отвергаем Н₀ в пользу Н₁ и ошибаемся в 3% случаев. Много это или мало, позволяет решить заранее выбранное граничное значение. Благодаря Роналду Фишеру, в большинстве случаев граничное значение p-value берут равным 0,05 [14]. Возвращаясь к примеру и опираясь на границу 0,05, для p-value 0,03 мы можем уверенно заключить, что сравниваемые выборки разные.

Анализ исходных данных

Выбор метода статистического анализа исходных данных зависит от их типа и характера распределения. Выделяют количественные и качественные данные². Количественные данные характеризуют величину явления или число объектов: например, лучевую нагрузку в миллизивертах при проведении КТ-исследования органов грудной клетки. Качественные, или категориальные, данные описывают отношение исследуемого явления к определённой группе: например, пол пациента или категория по шкале «КТ0–4».

При анализе данных в дополнение к основной гипотезе исследования всегда необходимо проверять ещё одну Н₀: «Данные распределены нормально». Нормальное распределение ― одно из самых важных в области статистики, поскольку часто встречается в возникающих естественным путём явлениях: ему подчиняются рост, вес, размер обуви, а также большое количество других характеристик популяции. Нормальное распределение описывается всего двумя параметрами ― средним значением и среднеквадратичным отклонением, и это допущение лежит в основе ряда статистических подходов к проверке гипотез.

Выбор метода проверки распределения на нормальность ― задача, не имеющая единственного решения на все случаи жизни. Так, X. Romão и соавт. [15] провели сравнение 33 таких методов и предложили оптимальные решения в зависимости от типа данных. Следует отметить, что выбор метода также зависит от размера исследуемой выборки [16], при этом самыми популярными являются критерий Колмогорова–Смирнова и тест Шапиро–Уилка [17].

Проверка нулевой гипотезы исследования

Помимо типа данных в сравниваемых выборках, корректный метод статистического анализа должен учитывать количество сопоставляемых групп, а также наличие связи между ними. Например, получены ли данные КТ- и НДКТ-исследований для одного и того же пациента или у разных. Различных статистических тестов разработано уже более 50, и для выбора оптимального метода существуют специальные онлайн-ресурсы³.

В нашем примере выборки парные, так как КТ- и НДКТ-данные получены последовательно для одних и тех же пациентов. При нормальном распределении целесообразно использовать парный t-критерий Стьюдента, а критерий Уилкоксона ― при распределении, отличном от нормального.

ПРАКТИЧЕСКИЙ ПРИМЕР

Для проведения статистического анализа были установлены программный пакет R (версия 4.2.2, https://cloud.r-project.org/) и интерфейс Posit (версия 353, https://posit.co/download/rstudio-desktop/, ранее RStudio).

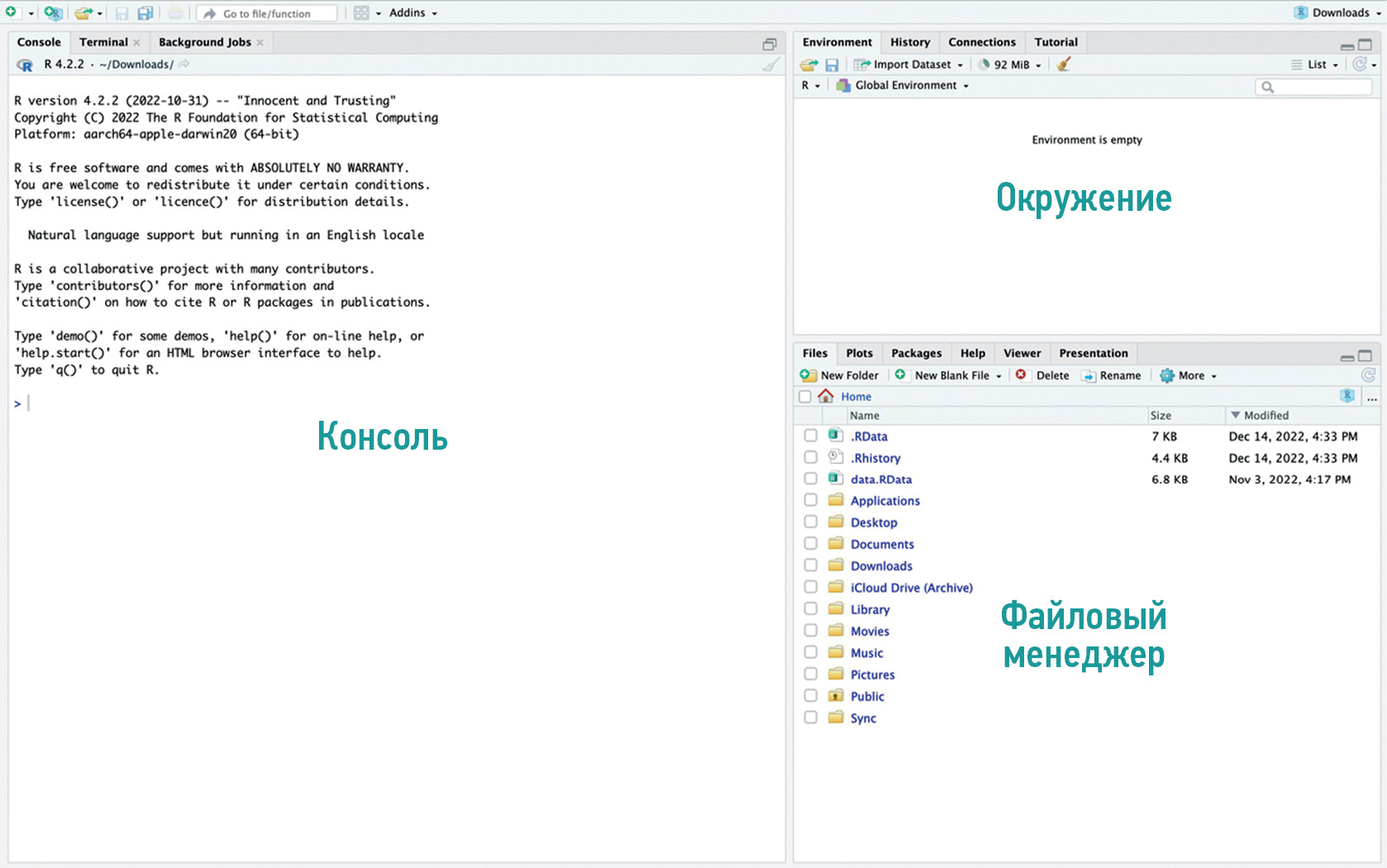
1. Базовый интерфейс Posit можно разделить на консоль (console), окружение (environment) и файловый менеджер (files) (рис. 1).

Рис. 1. Интерфейс программы Posit с указанием областей консоли, окружения и файлового менеджера.

 

Импорт данных осуществляется посредством опции File-Import Dataset. В нашем случае производился импорт таблицы Excel, содержащей данные об эффективных дозах КТ и НДКТ.

После импорта интерфейс программы изменится: в блоке окружения будет отображаться переменная с именем «data» (рис. 2). В левом верхнем квадранте появится также новая область ― блок просмотра данных, в котором будет отображаться загруженная таблица. Сравниваемые колонки в таблице названы как «Effective Dose (CT)» и «Effective Dose (LDCT)». Использование латиницы в названиях колонок позволяет избежать проблем с кодировкой и некорректным отображением символов в Posit.

 

Рис. 2. Интерфейс Posit после импорта файла: в левом верхнем квадранте экрана появилось окно с загруженными столбцами набора данных, а в правом верхнем квадранте указано количество столбцов (variables) и строк (obs., от англ. observations ― наблюдения).

 

Для удобства дальнейшей работы для каждой из этих колонок создадим отдельную переменную, выполнив в консоли команды, приведённые на рис. 3.

 

Рис. 3. Создание отдельной переменной для эффективной дозы компьютерной томографии с указанием функции каждого элемента команды.

 

Использование оператора «$» (см. рис. 3) отображает выпадающее меню столбцов в импортированной таблице, облегчающее ввод команды. После создания переменных они будут отображаться в правом верхнем квадранте интерфейса как «values» (рис. 4).

 

Рис. 4. Окно Posit после импорта файла и присвоения значений переменным: в правом верхнем квадранте появились новые переменные с предпросмотром первых пяти значений в каждой, в левом нижнем квадранте ― консольный интерфейс для выполнения команд.

 

2. Проверка нормальности распределения загруженных данных тестом Шапиро–Уилка осуществляется командой shapiro.test (рис. 5).

 

Рис. 5. Область с консольным интерфейсом Posit. Проверка нормальности распределения данных тестом Шапиро–Уилка.

 

Полученные p-value для обеих переменных значительно меньше выбранного граничного значения p=0,05, поэтому распределение данных для эффективной дозы как для КТ, так и НДКТ отличается от нормального. Следовательно, для проверки основной гипотезы исследования целесообразно использовать критерий Уилкоксона.

3. Проверка нулевой гипотезы для связанных количественных выборок с распределением данных, отличных от нормального, выполняется командой wilcox.test (рис. 6, 7).

 

Рис. 6. Проведение теста Уилкоксона с указанием функции каждого элемента команды.

 

Рис. 7. Проверка нулевой гипотезы исследования с помощью критерия Уилкоксона.

 

Полученное p-value значительно меньше выбранного граничного значения p=0,05, поэтому Н₀ можно отвергнуть в пользу Н₁. Это означает, что лучевая нагрузка при КТ и НДКТ статистически значимо отличается.

ЗАКЛЮЧЕНИЕ

Основная задача изложенного материала ― познакомить читателя с интерфейсом Posit и базовым функционалом языка R на практическом примере решения реальной медицинской задачи.

В работе кратко обобщены теоретические подходы к обработке медицинских данных, а также рекомендации по корректной формулировке задач исследования и выбора оптимальных методов статистического анализа.

Представленный материал может быть полезен на начальном этапе освоения статистического анализа с помощью инструментов языка R.

ДОПОЛНИТЕЛЬНО

Источник финансирования. Данная статья подготовлена авторским коллективом в рамках научно-практического проекта в сфере медицины (№ ЕГИСУ: 123031500005-2) «Научное обоснование методов лучевой диагностики опухолевых заболеваний с использованием радиомического анализа».

Конфликт интересов. Авторы заявляют об отсутствии явных и потенциальных конфликтов интересов, связанных с публикацией настоящей статьи.

Вклад авторов. Все авторы подтверждают соответствие своего авторства международным критериям ICMJE (все авторы внесли вклад в разработку концепции, проведение поисково-аналитической работы и подготовку статьи, прочли и одобрили финальную версию перед публикацией). Наибольший вклад распределён следующим образом: И.А. Блохин ― написание текста статьи, редактирование и утверждение итогового варианта текста рукописи; М.Р. Коденко, Ю.Ф. Шумская, А.П. Гончар ― редактирование и утверждение итогового варианта текста рукописи; Р.В. Решетников ― редактирование и утверждение итогового варианта текста рукописи, консультативная поддержка.

ADDITIONAL INFORMATION

Funding source. This article was prepared by a group of authors as a part of the medical research project (No. USIS [in the Unified State Information System for Accounting of Research, Development, and Technological Works]: 123031500005-2) «Scientific rationale for diagnostic radiology in oncology using radiomics».

Competing interests. The authors declare that they have no competing interests.

Authors’ contribution. All authors made a substantial contribution to the conception of the work, acquisition, analysis, interpretation of data for the work, drafting and revising the work, final approval of the version to be published and agree to be accountable for all aspects of the work. I.A. Blokhin ― writing the text of the article, editing and approval of the final version of the text of the manuscript; M.R. Kodenko, Yu.F. Shumskaya, A.P. Gonchar ― editing and approval of the final version of the text of the manuscript; R.V. Reshetnikov ― editing and approval of the final version of the text of the manuscript, advisory support.

¹ JAMA guide to statistics and methods [Electronic resource]. Режим доступа: https://jamanetwork.com/collections/44042/jama-guide-to-statistics-and-methods.

² Медицинская статистика [электронный ресурс]. Общие вопросы статистики. Режим доступа: https://medstatistic.ru/statistics/statistics3.html.

³ Statistics online--checks assumptions, interprets results (https://www.statskingdom.com/); Медицинская статистика. Выбор метода статистического анализа (https://medstatistic.ru/calculators/calcchoice.html).

Об авторах

Иван Андреевич Блохин

Научно-практический клинический центр диагностики и телемедицинских технологий

Email: i.blokhin@npcmr.ru
ORCID iD: 0000-0002-2681-9378
SPIN-код: 3306-1387
Россия, Москва

Мария Романовна Коденко

Научно-практический клинический центр диагностики и телемедицинских технологий; Московский государственный технический университет имени Н.Э. Баумана (национальный исследовательский университет)

Email: KodenkoMR@zdrav.mos.ru
ORCID iD: 0000-0002-0166-3768
SPIN-код: 5789-0319
Россия, Москва; Москва

Юлия Федоровна Шумская

Научно-практический клинический центр диагностики и телемедицинских технологий; Первый Московский государственный медицинский университет имени И.М. Сеченова (Сеченовский Университет)

Email: ShumskayaYF@zdrav.mos.ru
ORCID iD: 0000-0002-8521-4045
SPIN-код: 3164-5518
Россия, Москва; Москва

Анна Павловна Гончар

Научно-практический клинический центр диагностики и телемедицинских технологий

Email: a.gonchar@npcmr.ru
ORCID iD: 0000-0001-5161-6540
SPIN-код: 3513-9531
Россия, Москва

Роман Владимирович Решетников

Научно-практический клинический центр диагностики и телемедицинских технологий

Автор, ответственный за переписку.
Email: r.reshetnikov@npcmr.ru
ORCID iD: 0000-0002-9661-0254
SPIN-код: 8592-0558

к.ф.-м.н.

Россия, Москва

Список литературы

Дополнительные файлы