使用R语言进行研究假设检验

封面图片


如何引用文章

全文:

详细

对于现代科学家来说，统计数据处理的能力越来越重要。用于统计分析的开源软 件（open-source software）的明显优势是可用性和多功能性。在免费的解决方案中， R语言和相关软件大有可为，可作为一个最简控制台界面或作为一个完全合格的开发环境RStudio/Posit。

我们提供一份使用R语言工具比较两组数据的实用指南，以COVID-19的标准电子计算机断层扫描和低剂量电脑断层扫描的有效剂量比较为例。本指南简略地总结了医学数据处理的理论方法，以及正确制定研究目标和选择最佳统计分析方法的建议。

本实用指南的主要目的是通过一个解决真实医学问题的实际例子向读者介绍Posit界面和R语言的基本功能。所介绍的材料在借助R语言工具掌握统计分析的初始阶段可以有益处。

全文:

绪论

统计数据处理正在成为现代科学家的一项重要技能。1983年，读者只要知道描述性统计的基本概念（百分比、平均数和标准差）和统计假设检验的一种方法（学生t检验，亦称t检验）就足够了[1]。这些知识使我们能够理解著名的《新英格兰医学杂志》（New England Journal of Medicine）的760篇科学出版物中的三分之二。随着时间的推移，科学界面临了这种数据分析方法的局限性。2014年，《美国医学会杂 志》（Journal of American Medical Association）宣布了一系列特种刊物1，包括为临床医生解释统计分析方法的文章在内。如今，可以找到开放获取的概述性文章，不仅涉及数据分析的基本方面[2]，而且还涉及选择适当的数据处理方法[3]。此外，关于在生物医学研究中使用统计方法的详细清单（生物医学研究中的统计分析方法，Statistical Analysis Methods in Biomedical Research）[4]是于2019年出版的。然而，要不是积极开展自动化软件，数据分析方法的实际应用将很困难。

鉴于大量的收费统计分析软件和商业提供的全面数据处理服务，开源软件（open-source software）的明显优势是可用性和多功能性[5] 。 在免费的解决方案中，R语言和相关软件大有可为 [6]，可作为一个最简控制台界面[7]或作为一个完全合格的开发环境RStudio/Posit[8]。

本文章的目的是通过一个解决真实医学问题的实际例子向读者介绍R语言的基本操作：比较患者在COVID-19的标准电子计算机断层扫描（CT）和低剂量电脑断层扫描（LDCT）期间接受的有效剂量。该任务的现实性在于监测辐射暴露的必 要[9]（因为放射检查的数量不断增加[10]）， 以及因此在于LDCT协议的开展[11]和临床证 明[12 ，13]的重要性。

在进行统计分析时，需要遵循一些基本步骤。

问题陈述和分析的无效假设的提出

无效假设是统计分析的出发点。在比较两组数据时，无效假设（H0）的表述如下：“没有统计学意义的差异”。在这个例子中，对患者在COVID-19的标准电子计算机断层扫描（CT）和低剂量电脑断层扫描（LDCT）期间接受的有效剂量进行了比较。换句话说，这项任务的H0的表述是：“CT和LDCT的辐射暴露是相当的”。

还要记住“替代假设”（H1）。H1 是H0的拮抗假说。它们应该是相互排斥的。在这个例子中，替代假设H1将是：“在CT和LDCT中，COVID-19患者的有效剂量有统计学意义的差异”。

统计学中的无效假设检验的结果是所谓的 p值（p-value），即错误地拒绝H0的概率。这个值可以解释为如下：“如果我们多次重复实验并拒绝无效假设，那么在100%的场合下，我们会对p值的看法错”。例如，对于0.03的p值，我们拒绝H0 ，支持H1，并且在3%的场合下犯错误。一个预选的边界值可以让我们决定是很多还是很少。感谢罗纳德·费舍尔，在大多数场合下，采取的边界值是0.05的p值[14]。回到这个例子，依靠0.05的边界值，对于0.03的p值，我们可以有把握地得出结论：被比较的样本是不同的。

原始数据的分析

对原始数据进行统计分析的方法的选择取决于数据类型和分布性质。数据分为定量数据和定性数据2。定量数据描述一个现象的大小或对象的数量。例如，胸部CT的辐射暴露，单位为毫西弗。定性数据或分类数据描述有关现象属于某一特定的群体。例如，患者性别或CT分级0-4级的一个类别。

在分析数据时，除了研究的主要假设外，总是有必要检验另一个假设（H0）：“数据服从正态分布”。正态分布是统计学领域中最重要的性质之一。正态分布经常出现在自然发生的现象中。身高、体重、鞋码和人口和大量的其他群体特征都服从正态分布。正态分布仅由两个参数描述，即平均值和标准差。这一假设是一系列假设检验的统计方法的基础。

选择一种方法来检验正态分布的任务没有一个放之四海而皆准的解决方案。因此，X.Romão等人[15]对33种此类方法进行了比较。他们根据数据的类型提出了最佳解决方案。值得注意的是，方法的选择也取决于所研究的样本容量[16]。最受欢迎的是柯尔莫哥洛夫-斯米尔诺夫检验和夏皮罗-威尔克检验[17]。

研究中的无效假设检验

正确的统计分析方法应该考虑到被比较的样本中的数据类型、被比较的组数，以及它们之间是否存在关系。例如，正确的方法应该考虑到CT和LDCT的数据是来自同一个病人还是来自不同的病人。目前已经开发了50多种不同的统计测试。有专门的在线资源3被用于选择最佳方法。

在该例子中，我们使用了成对样本，因为CT和LDCT数据是为同一病人连续获得的。成对t检验适用于正态分布。威尔科克森符号秩检验适合于非正态分布的情况。

实例

我们安装了R软件包（版本4.2.2，https://cloud.r-project.org/）和Posit界面（版本353，https://posit.co/download/rstudio-desktop/，前身为RStudio），以进行统计分析。

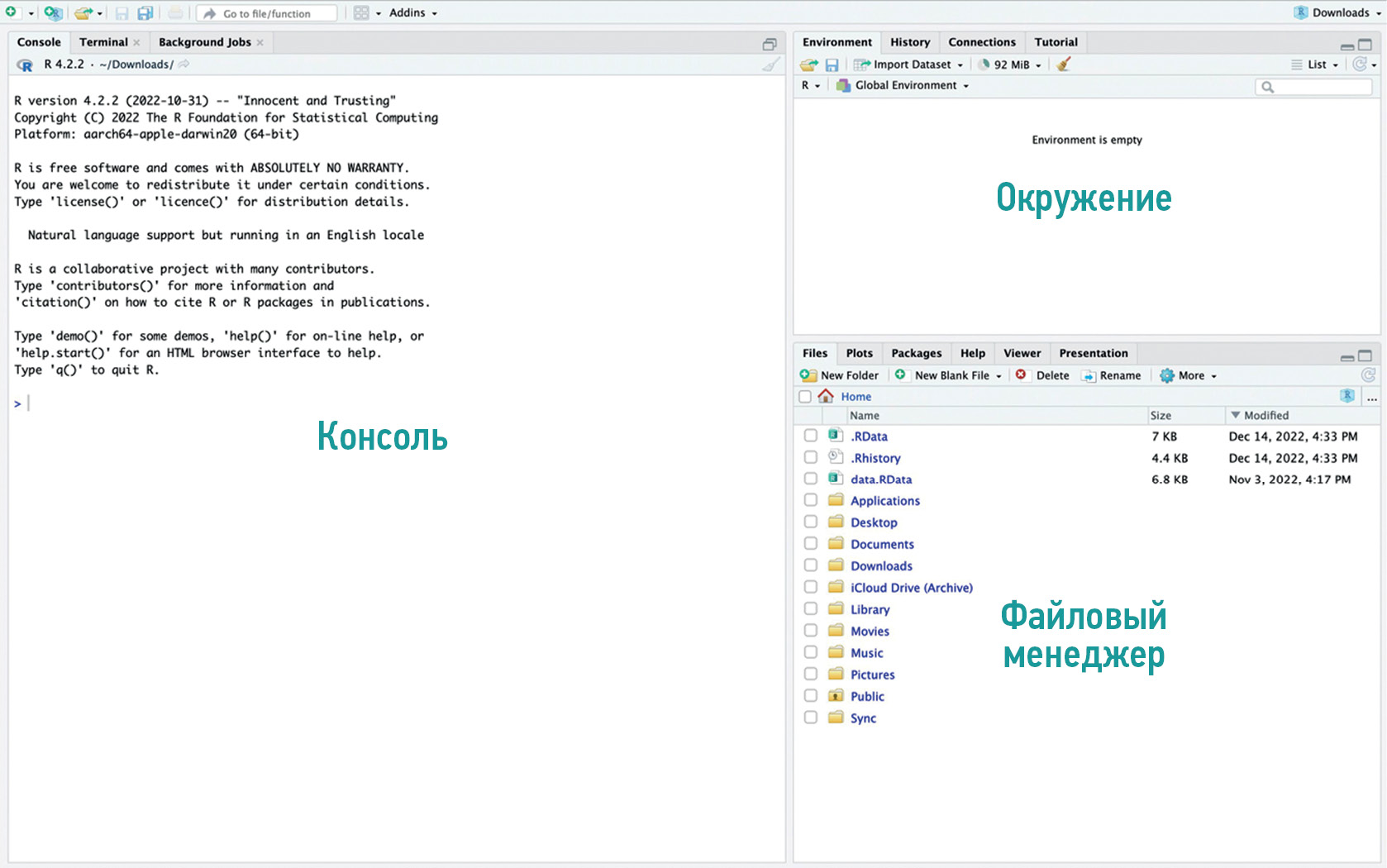
1. Posit的基本界面可以分为控制台（console） 、环 境（environment）和文件管理器（files）（图1） 。

 

图1。Posit界面，显示控制台、环境和文件管理器的区域。

 

使用File-Import Dataset选项来导入数据。我们导入了一个包含CT和LDCT有效剂量数据的Excel电子表格。

导入后，程序界面将发生变化。名为“data”的变量将出现在环境中（图2）。同时，一个新的区域，即数据视图部件，将出现在左上角的象限中。加载的表格将出现在这里。表中要比较的列被命名为“Effective Dose（CT）”和 “ Effective Dose（LDCT）”。在列名中使用拉丁字符允许避免编码问题和Posit中字符的不正确显示。

 

图2。导入文件后的Posit界面：在屏幕上的左上象限中出现了一个加载了数据集列的窗口，在右上象限中显示了列数（variables）和行数（obs.，来自英语的observations——观察资料）。

 

为了进一步工作的方便，让我们通过在图3所示的控制台中运行命令为每一列创建一个单独的变量。

使用“$”运算符（见图3）会在导入的表格中显示一个列的下拉菜单，以减轻命令输入。创建变量之后，它们将出现在右上角的象限中，名为“values”（图4）。

 

图3。为CT有效剂量创建一个单独的变量，显示每个指令元素的功能。

 

图4。导入文件并指定变量后的Posit窗口：在右上象限中出现了新变量，每个变量的前五个数值都有预览；在左下象限中出现了执行命令的控制台界面。

 

2. 为了检验加载数据的正态分布，通过shapiro.test命令使用夏皮罗-威尔克检 验（图5）。

 

图5。带有Posit控制台界面的区域。通过夏皮罗-威尔克检验进行的数据正态分布检验。

 

得出的两个变量的p值都明显小于选择的p值为0.05的边界值，所以CT和LDCT的有效剂量的数据分布与正常值不同。因此，使用威尔科克森符号秩检验来检验本研究的主要假设是合适的。

3. 对于非正态分布的相关定量样本，通过wilcox.test命令进行无效假设检验（图6，7）。

 

图6。进行威尔科克森符号秩检验，显示每个指令元素的功能。

 

图7。通过威尔科克森符号秩检验进行无效假设检验。

 

由此得出的p值明显小于选择的p值为0.05的边界值。因此，可以拒绝H0，支持H1。这意味着CT和LDCT的辐射暴露数据有统计学意义的差异。

结论

本文章的主要目的是通过一个解决真实医学问题的实际例子向读者介绍Posit界面和R语言的基本功能。

本文简略地总结了医学数据处理的理论方法，以及正确制定研究目标和选择最佳统计分析方法的建议。

所介绍的材料在借助R语言工具掌握统计分析的初始阶段可以有益处。

ADDITIONAL INFORMATION

Funding source. This article was prepared by a group of authors as a part of the medical research project (No. USIS [in the Unified State Information System for Accounting of Research, Development, and Technological Works]: 123031500005-2) «Scientific rationale for diagnostic radiology in oncology using radiomics».

Competing interests. The authors declare that they have no competing interests.

Authors’ contribution. All authors made a substantial contribution to the conception of the work, acquisition, analysis, interpretation of data for the work, drafting and revising the work, final approval of the version to be published and agree to be accountable for all aspects of the work. I.A. Blokhin ― writing the text of the article, editing and approval of the final version of the text of the manuscript; M.R. Kodenko, Yu.F. Shumskaya, A.P. Gonchar ― editing and approval of the final version of the text of the manuscript; R.V. Reshetnikov ― editing and approval of the final version of the text of the manuscript, advisory support.

×

作者简介

Ivan A. Blokhin

Moscow Center for Diagnostics and Telemedicine

Email: i.blokhin@npcmr.ru
ORCID iD: 0000-0002-2681-9378
SPIN 代码: 3306-1387
俄罗斯联邦, Moscow

Maria R. Kodenko

Moscow Center for Diagnostics and Telemedicine; Bauman Moscow State Technical University

Email: KodenkoMR@zdrav.mos.ru
ORCID iD: 0000-0002-0166-3768
SPIN 代码: 5789-0319
俄罗斯联邦, Moscow; Moscow

Yuliya F. Shumskaya

Moscow Center for Diagnostics and Telemedicine; The First Sechenov Moscow State Medical University

Email: ShumskayaYF@zdrav.mos.ru
ORCID iD: 0000-0002-8521-4045
SPIN 代码: 3164-5518
俄罗斯联邦, Moscow; Moscow

Anna P. Gonchar

Moscow Center for Diagnostics and Telemedicine

Email: a.gonchar@npcmr.ru
ORCID iD: 0000-0001-5161-6540
SPIN 代码: 3513-9531
俄罗斯联邦, Moscow

Roman V. Reshetnikov

Moscow Center for Diagnostics and Telemedicine

编辑信件的主要联系方式.
Email: r.reshetnikov@npcmr.ru
ORCID iD: 0000-0002-9661-0254
SPIN 代码: 8592-0558

Cand. Sci. (Phys-Math)

俄罗斯联邦, Moscow

参考

  1. Emerson J, Colditz GA. Use of statistical analysis in the New England Journal of Medicine. New Engl J Med. 1983;309(12):709–713. doi: 10.1056/NEJM198309223091206
  2. Ali Z, Bhaskar SB. Basic statistical tools in research and data analysis. Indian J Anaesth. 2016;60(9):662–669. doi: 10.4103/0019-5049.190623
  3. Mishra P, Pandey CM, Singh U, et al. Selection of appropriate statistical methods for data analysis. Ann Card Anaesth. 2019;22(3):297–301. doi: 10.4103/aca.ACA_248_18
  4. Dwivedi AK, Shukla R. Evidence-based statistical analysis and methods in biomedical research (SAMBR) checklists according to design features. Cancer Rep (Hoboken). 2020;3(4):e1211. doi: 10.1002/cnr2.1211
  5. Rigby PC, German DM, Cowen L, et al. Peer review on open-source software projects: Parameters, statistical models, and theory. ACM Trans Softw Eng Methodol. 2014;23(4):35.
  6. Culpepper SA, Aguinis H. R is for revolution: A cutting-edge, free, open source statistical package. Organizational Research Methods. 2011;14(4):735–740.
  7. Ihaka R, Gentleman R. R: A language for data analysis and graphics. J Computational Graphical Statistics. 1996;5(3):299–314. doi: 10.1080/10618600.1996.10474713
  8. Niu G, Segall RS, Zhao Z, et al. A survey of open source statistical software (OSSS) and their data processing functionalities. Int J Open Source Software Processes. 2021;12(1):1–20. doi: 10.4018/IJOSSP.2021010101
  9. Shatenok MP, Ryzhov SA, Lantukh ZA, et al. Patient dose monitoring software in radiology. Digital Diagnostics. 2022;3(3):212–230. (In Russ). doi: 10.17816/DD106083
  10. Druzhinina UV, Ryzhov SA, Vodovatov AV, et al. Coronavirus Disease-2019: Changes in computed tomography radiation burden across Moscow medical facilities. Digital Diagnostics. 2022;3(1):5–15. (In Russ). doi: 10.17816/DD87628
  11. Gombolevskiy V, Morozov S, Chernina V, et al. A phantom study to optimise the automatic tube current modulation for chest CT in COVID-19. Eur Radiol Exp. 2021;5(1):21. doi: 10.1186/s41747-021-00218-0
  12. Blokhin I, Gombolevskiy V, Chernina V, et al. Inter-observer agreement between low-dose and standard-dose CT with soft and sharp convolution kernels in COVID-19 pneumonia. J Clin Med. 2022;11(3):669. doi: 10.3390/jcm11030669
  13. Blokhin IA, Gonchar AP, Kodenko M, et al. Impact of body mass index on the reliability of the CT0–4 grading system: A comparison of computed tomography protocols. Digital Diagnostics. 2022;3(2):108–118. (In Russ). doi: 10.17816/DD104358
  14. Kennedy-Shaffer L. Before p<0.05 to beyond p<0.05: Using history to contextualize p-values and significance testing. Am Stat. 2019;73(Suppl. 1):82–90. doi: 10.1080/00031305.2018.1537891
  15. Romão X, Delgado R, Costa A. An empirical power comparison of univariate goodness-of-fit tests for normality. J Statist Computation Simulat. 2010;80(5):545–591. doi: 10.1080/00949650902740824
  16. Lumley T, Diehr P, Emerson S, Chen L. The Importance of the normality assumption in large public health data sets. Ann Rev Pub Health. 2002;23(1):151–169. doi: 10.1146/annurev.publhealth.23.100901.140546
  17. Mishra P, Pandey CM, Singh U, et al. Descriptive statistics and normality tests for statistical data. Ann Card Anaesth. 2019;22(1):67–72. doi: 10.4103/aca.ACA_157_18

补充文件

附件文件
动作
1. JATS XML
下载
2. 图1。Posit界面，显示控制台、环境和文件管理器的区域。

下载 (188KB)
索引源数据
3. 图2。导入文件后的Posit界面：在屏幕上的左上象限中出现了一个加载了数据集列的窗口，在右上象限中显示了列数（variables）和行数（obs.，来自英语的observations——观察资料）。

下载 (212KB)
索引源数据
4. 图3。为CT有效剂量创建一个单独的变量，显示每个指令元素的功能。

下载 (113KB)
索引源数据
5. 图4。导入文件并指定变量后的Posit窗口：在右上象限中出现了新变量，每个变量的前五个数值都有预览；在左下象限中出现了执行命令的控制台界面。

下载 (178KB)
索引源数据
6. 图5。带有Posit控制台界面的区域。通过夏皮罗-威尔克检验进行的数据正态分布检验。

下载 (173KB)
索引源数据
7. 图6。进行威尔科克森符号秩检验，显示每个指令元素的功能。

下载 (124KB)
索引源数据
8. 图7。通过威尔科克森符号秩检验进行无效假设检验。

下载 (114KB)
索引源数据

版权所有 © Eco-Vector, 2023

Creative Commons License
此作品已接受知识共享署名-非商业性使用-禁止演绎 4.0国际许可协议的许可。
СМИ зарегистрировано Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор).
Регистрационный номер и дата принятия решения о регистрации СМИ: серия ПИ № ФС 77 - 79539 от 09 ноября 2020 г.